Введение
Основные определения
Зачем это нужно?
Не редко случайный разброс используется при написании карт/игр. Начиная с выбора персонажа, дропа предмета, шанса крита, до генерации шума и создания карты высот.
Описание
Линейный конгруэнтный генератор
Использует простую формулу для получения последовательности:
Xn+1 = (a * Xn – c) mod M;
a, c, M – особые константы; X[0, M-1]; период <= M.
Xn+1 = (a * Xn – c) mod M;
a, c, M – особые константы; X[0, M-1]; период <= M.
Запаздывающий генератор Фибоначчи
Позволяет получить более высокое "качество" псевдослучайных чисел.
В данной реализации Ki:
{ Ki-a – Ki-b, если Ki-a >= Ki-b
{ Ki-a – Ki-b + 1, если Ki-a < Ki-b
a, b – особые константы; K[0, 1]; период = (2^max(a,b) - 1) * 2^l, где l число битов в мантиссе вещественного числа.
В данной реализации Ki:
{ Ki-a – Ki-b, если Ki-a >= Ki-b
{ Ki-a – Ki-b + 1, если Ki-a < Ki-b
a, b – особые константы; K[0, 1]; период = (2^max(a,b) - 1) * 2^l, где l число битов в мантиссе вещественного числа.
Функционал
- получить/установить зерно (для линейного конгруэнтного генератора);
- случайный real в диапазонах: [0,1], [0,max], [min,max];
- случайный int в диапазонах: [0,max], [min,max].
Linear Congruent Generator.w3m
Lagged Fibonacci Generator.w3m
Используется один генератор, выбираемый при инициализации.
Lagged Fibonacci Generator.w3m
Используется один генератор, выбираемый при инициализации.
Multi Linear Congruent Generator.w3m
Multi Lagged Fibonacci Generator.w3m
Тут можно создать "объект" генератора. Подходит, если вам нужно несколько одинаковых генераторов или несколько разных генераторов.
Multi Lagged Fibonacci Generator.w3m
Тут можно создать "объект" генератора. Подходит, если вам нужно несколько одинаковых генераторов или несколько разных генераторов.
источники:
Дополнительно
исследование генераторов
Сначала пытались исследовать встроенный генератор.
посмотрели его начальные значения, сымитировали работу.
посмотрели его начальные значения, сымитировали работу.
Обход генератора оказался слишком долгим,
поэтому отказываемся от любых сравнительных тестов и для работы выбираем генератор поменьше.
поэтому отказываемся от любых сравнительных тестов и для работы выбираем генератор поменьше.
Каждое число в нашем генераторе внутри 1 периода встречается 1 раз, совпадений нету.
Качество генератора зависит от качества перемешивания чисел.
Поверим автору статьи и его источникам (таблица хороших констант)
и переходим к другим важным прикладным вопросам.
Качество генератора зависит от качества перемешивания чисел.
Поверим автору статьи и его источникам (таблица хороших констант)
и переходим к другим важным прикладным вопросам.
требования:
Хочу рандом, чтобы 25%, чтобы четверть из ста ударов, но не рандом который контролируешь, а рандом который рандом, но 25%, может наука есть которая рандом изучает я хз
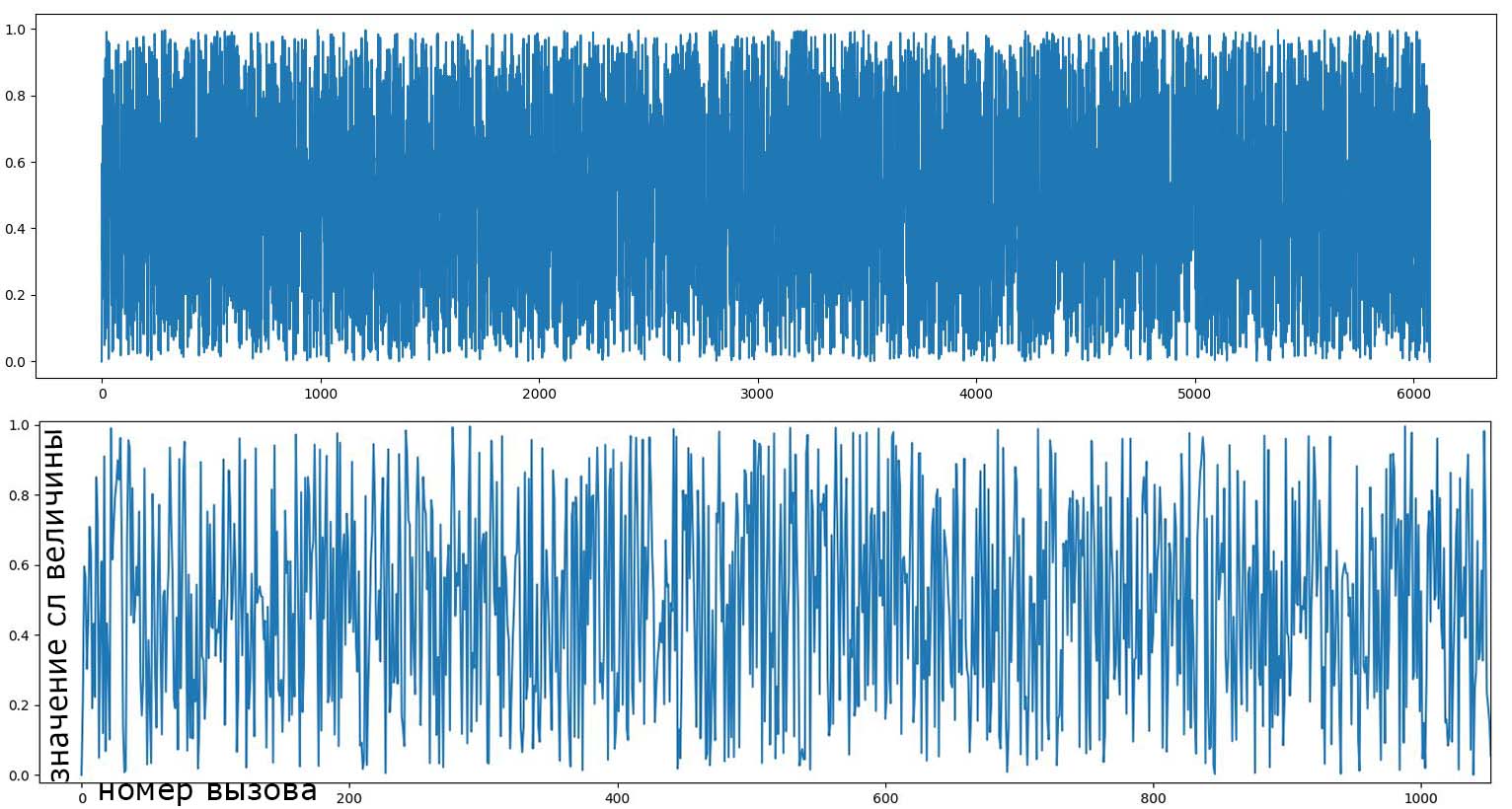
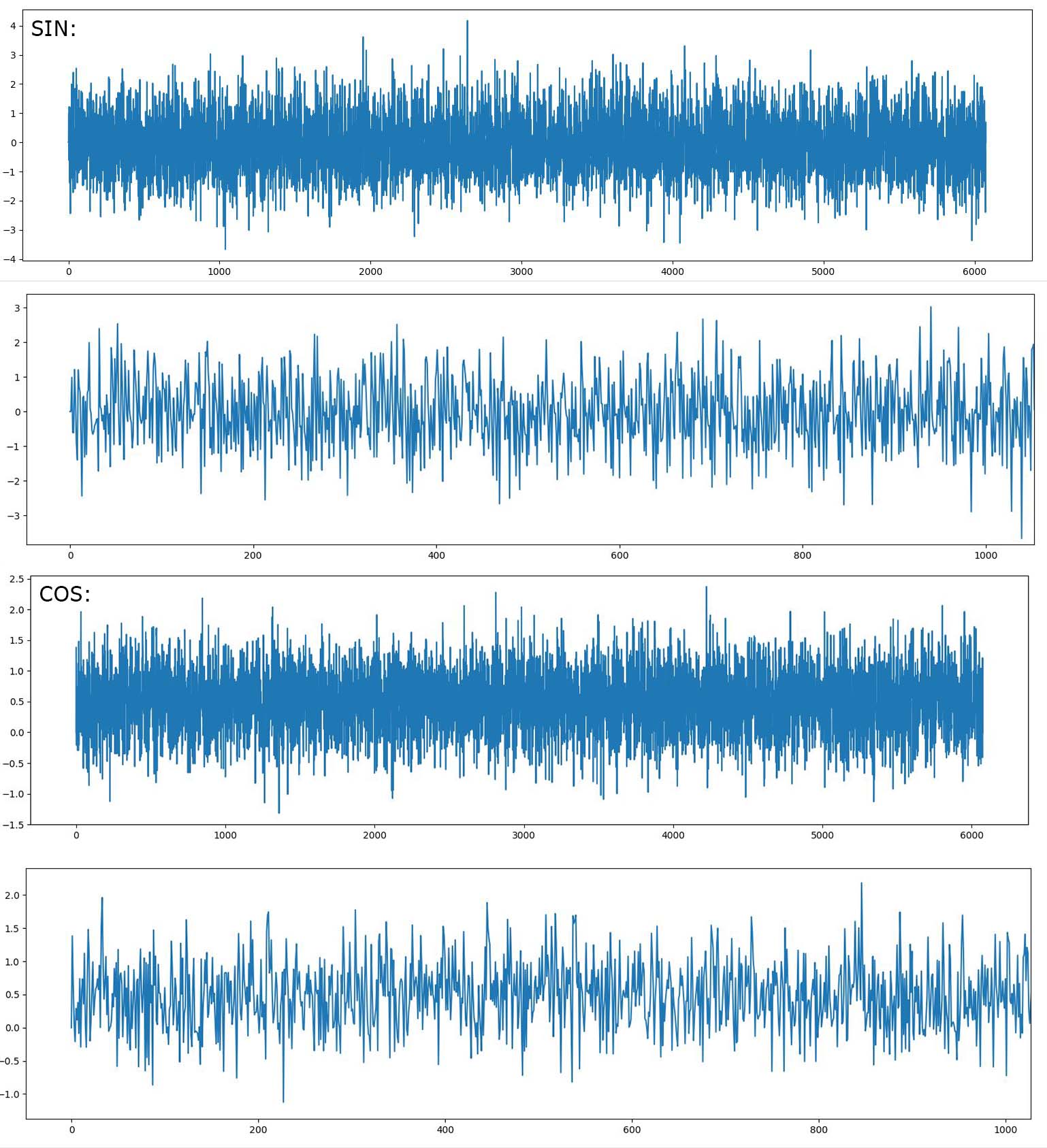
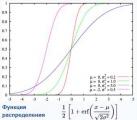
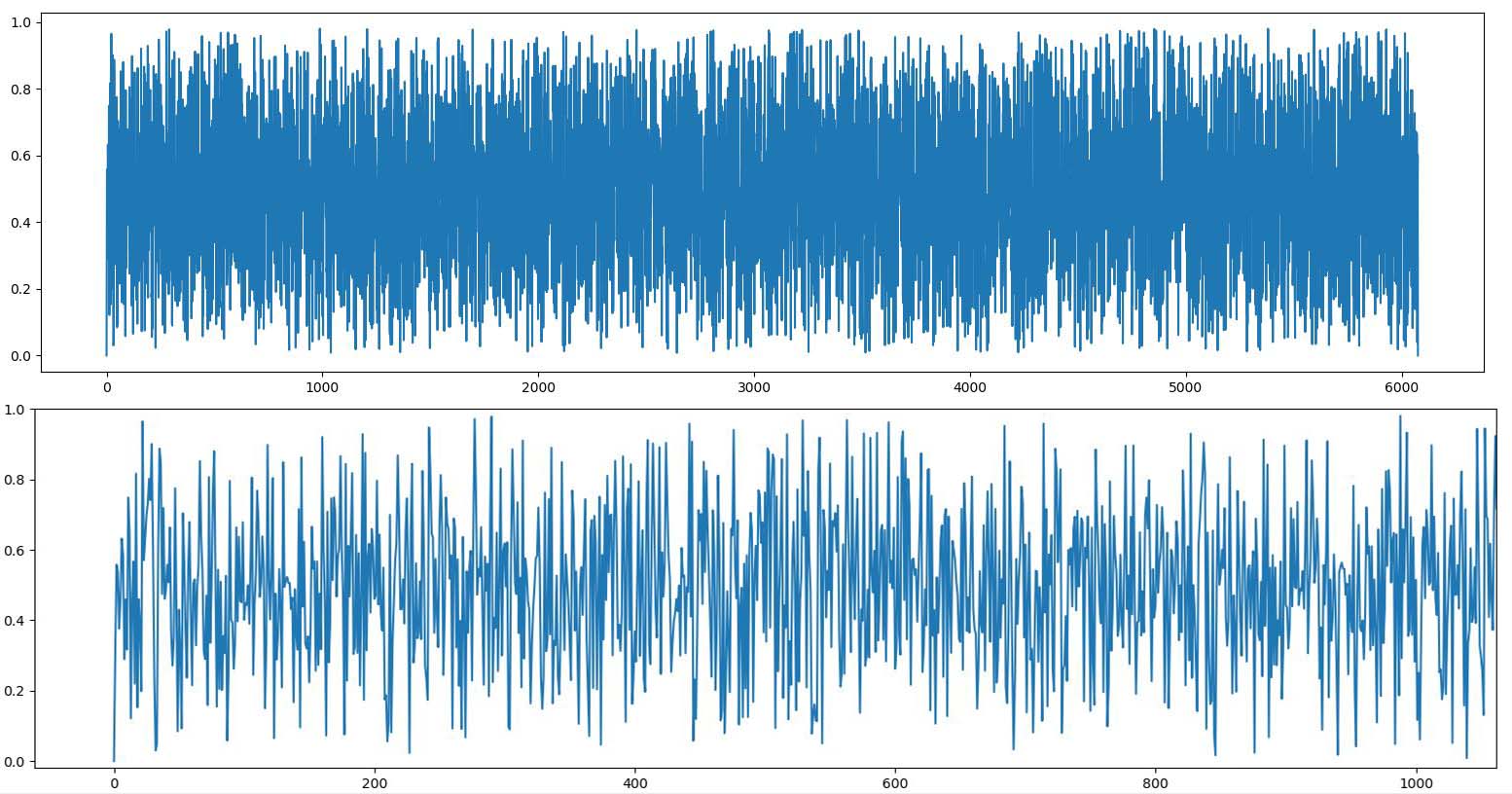
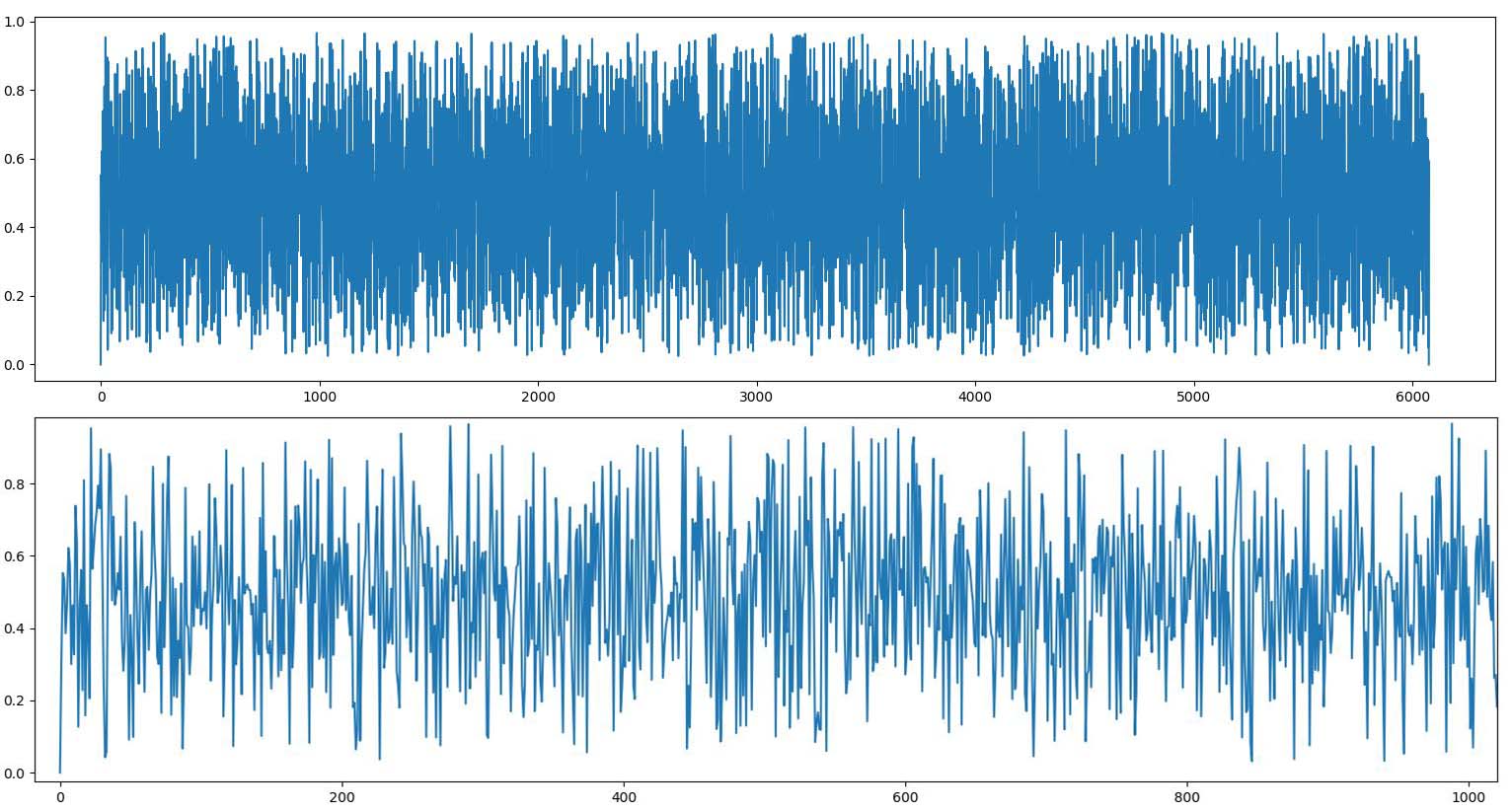
Наши генераторы имеют равномерное распределение. Значение случайной величины на всем диапазоне равновероятно, в отличии от нормального распределения.
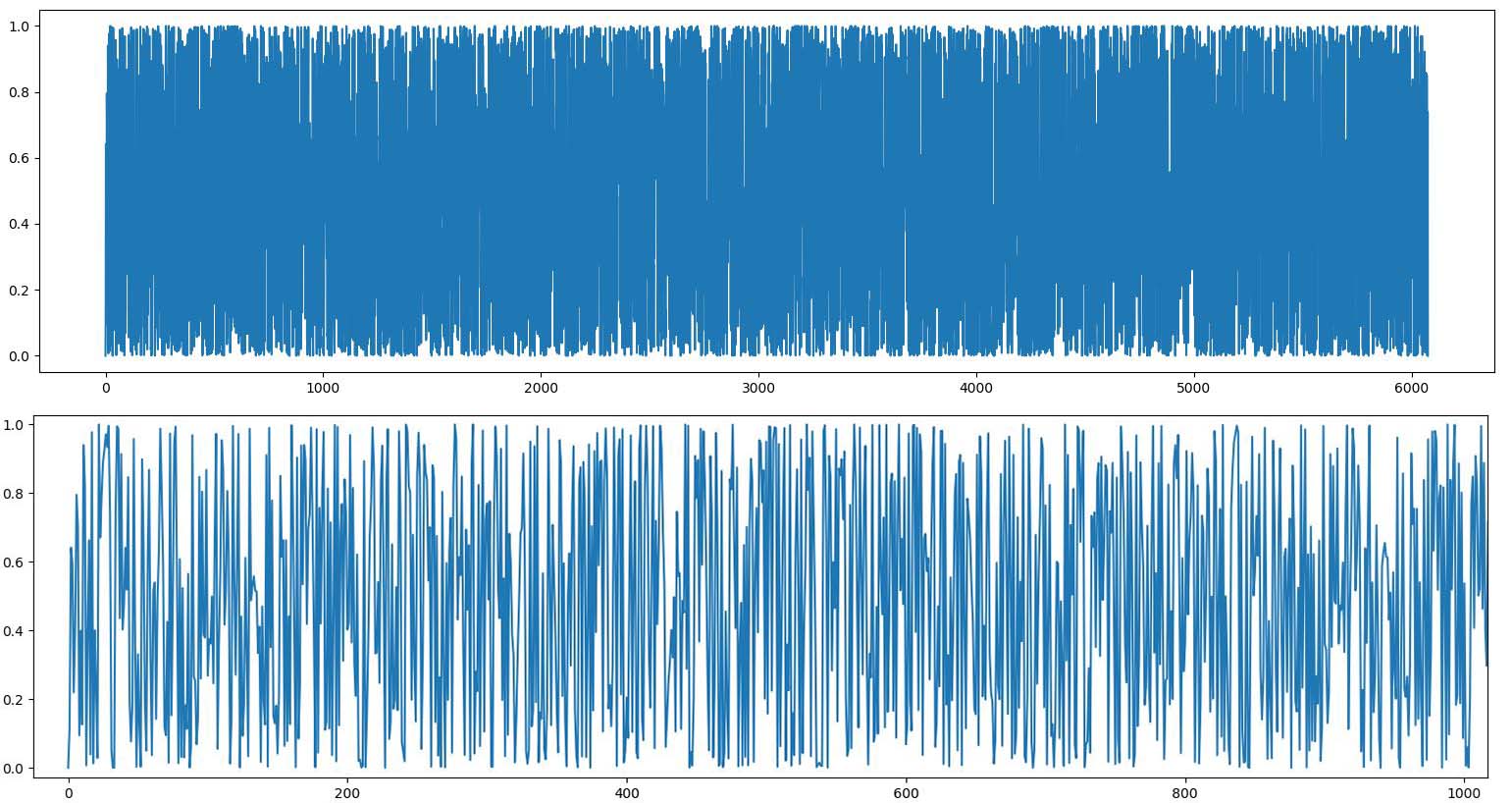
Смотрим на график - видим почти белый шум:
Реализуем первый вариант. Для r и f берем текущее и прошлое значение генератора.
Конечно, иногда может быть круто, задавая границы [0,50] получить в ответ 150.
Пробуем второй вариант:
Получаем слишком большой разброс, корректируем res=z1*z2 по примеру
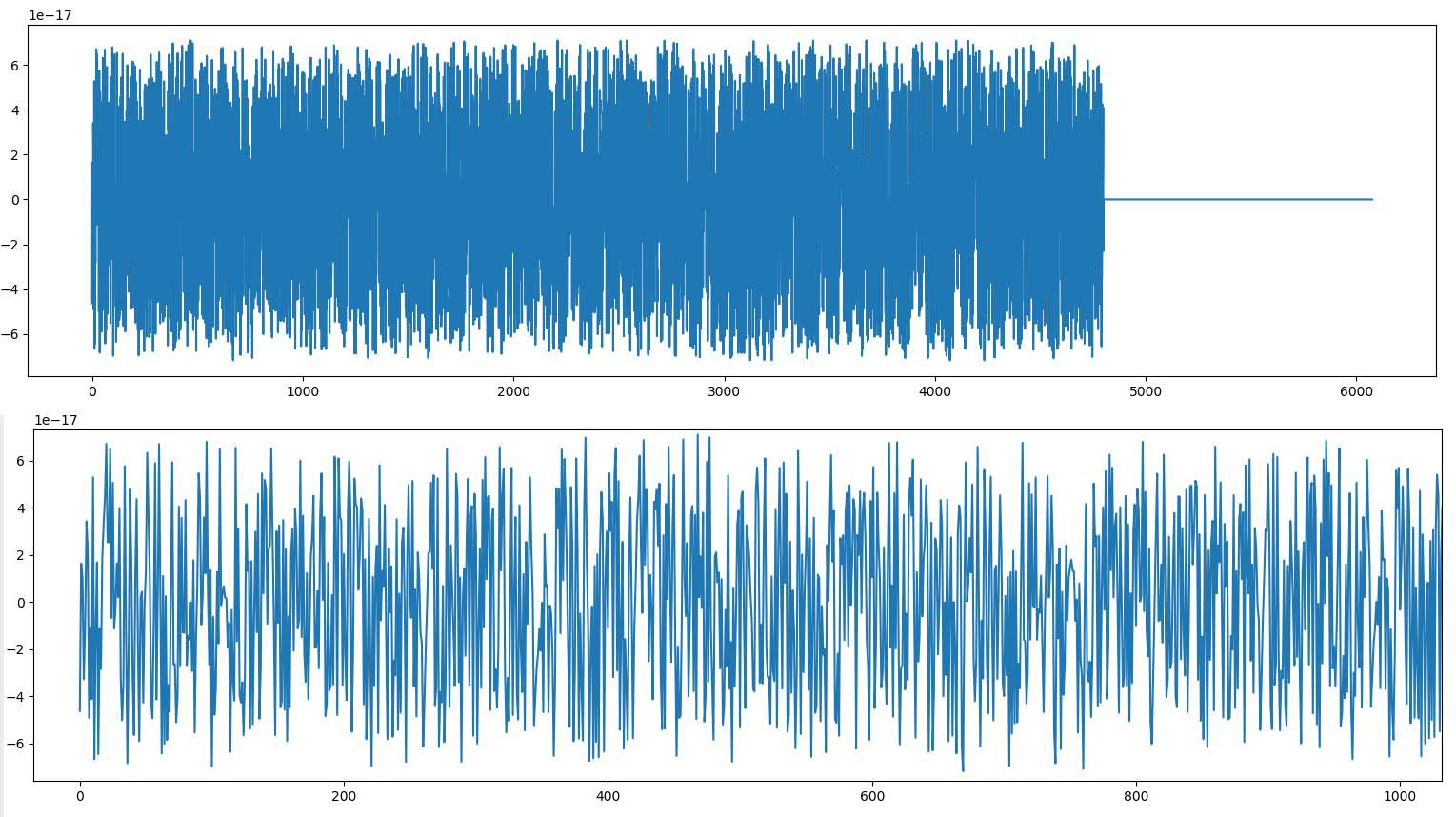
Визуально величина схожа с нормальной.
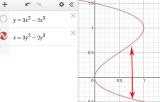
Нужны точные границы!
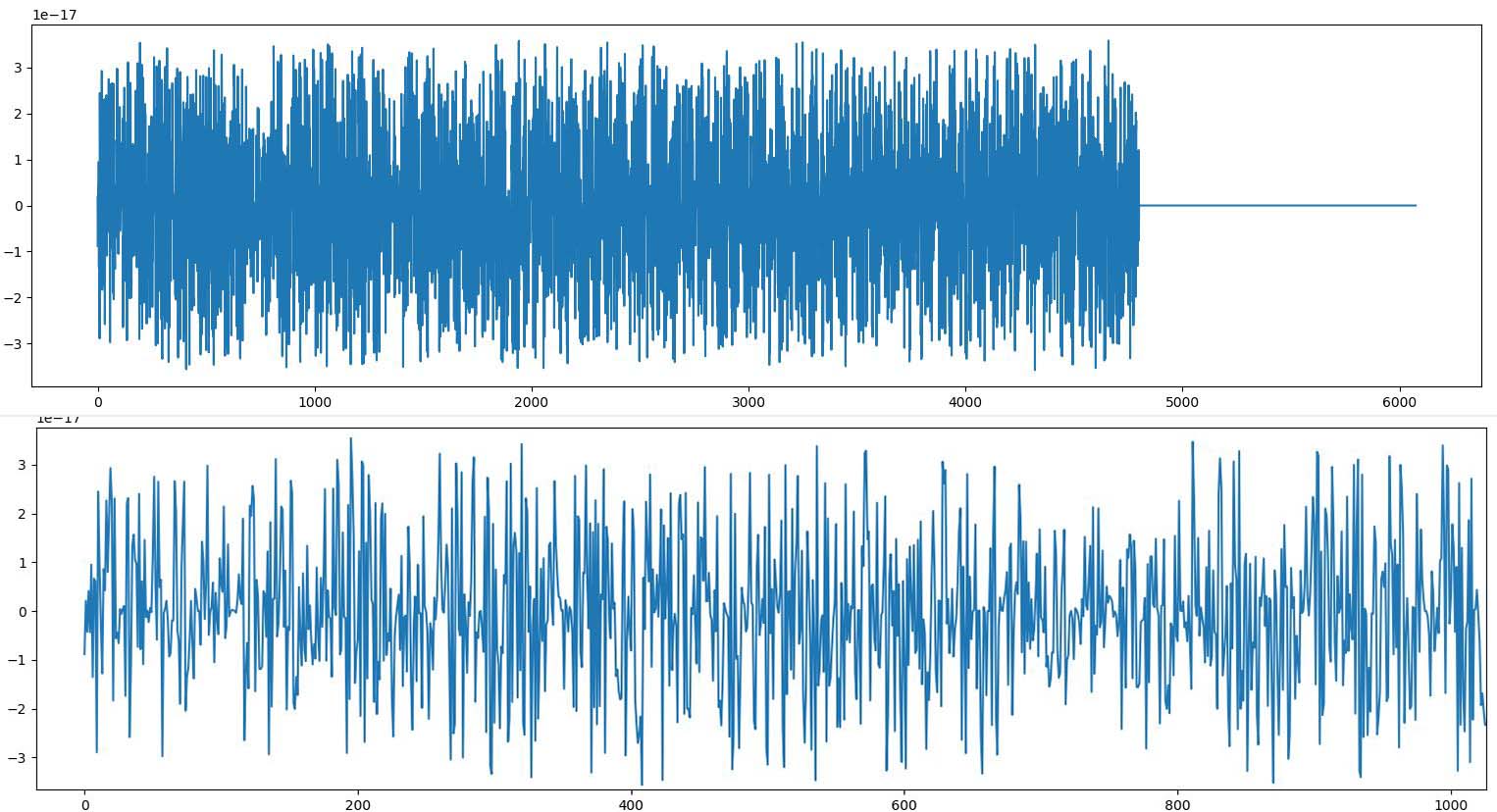
Видим, что график смещает случайную величину определенным образом.
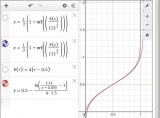
В формуле есть какая-то erf, нам такое не подходит.
Почему бы не заменить этот график на другой, достаточно точно совпадающий?
В формуле есть какая-то erf, нам такое не подходит.
Почему бы не заменить этот график на другой, достаточно точно совпадающий?
Самая простая функция такого вида что я видел была в статье о шуме Перлина, как сглаживающая функция. Smoothstep, открываем подраздел этих функций, берем первые 2 типа, смотрим:
Отлично, первая совпадает, строим графики:
Втф, что это. Шум явно изменился, и дело точно не в погрешности.
С помощью бумаги и ручки был создан набросок интересующей нас функции, которая должна сплющивать или стягивать значения к центру.
Сравнив это с тем, что мы делали, прояснилась ключевая ошибка.
Пошаманив над графиком, получилось.
Придется выражать обратную функцию, но со смузером это не прокатит.
Шел вечер пятницы, время поджимало.
Погрузившись в чертоги разума, вспомнились функции активации нейрона.
Подбираем за пару минут коэффициенты.
Погрузившись в чертоги разума, вспомнились функции активации нейрона.
Подбираем за пару минут коэффициенты.
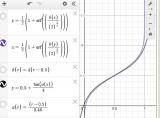
С утреца, подготавливая эти материалы, обнаружил список функций класса сигмоид. Оно и хорошо, логарифма то в варкрафте нет!
Результаты порадовали, впереди еще предстояла проверка других генераторов.
Результаты:
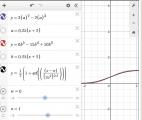
Для преобразования равномерного распределения в близкое к нормальному предлагается следующая формула: y = 0.5 + tan( (x-0.5)*2.17391 )*0.25
где y/x - новое/старое значение сл. величины [0,1]
где y/x - новое/старое значение сл. величины [0,1]
Заключение
почему не jass
Перегрузка функций;
Компактность и прозрачность кода.
Компактность и прозрачность кода.
об integer
Из-за отсутствия беззнакового типа допущение переполнения int может привести к неопределенному поведению, что накладывает некоторые ограничения на реализацию линейного конгруэнтного генератора.
тест на скорость
Тест оценивает, во сколько раз текущие генераторы сильнее нагружают лимит операций
относительно оригинальной функции. Эксперимент проводился с помощью:
относительно оригинальной функции. Эксперимент проводился с помощью:
code
integer INT = 0
function MyCode takes nothing returns nothing
// ...initialization
TriggerSleepAction(0.)
loop
//q = LCG_randr(g,20.,100.)
//i = LCG_randi(g,2,20)
INT++
endloop
endfunction
function PostMyCode takes nothing returns nothing
TriggerSleepAction(0.3)
printi(INT)
endfunctionРезультаты:
| \ | native | LCG | MLCG | LFG | MLFG |
|---|---|---|---|---|---|
| int(0,max) | 23076 (1) | 5172 (4.4) | 3896 (5.9) | 5660 (4) | 4225 (5.4) |
| int(min,max) | 21428 (1) | 4545 (4.7) | 3529 (6) | 4918 (4.3) | 3796 (5.6) |
| real(0,1) | 23076 (1) | 6382 (3.6) | 4545 (5) | 7142 (3.2) | 5000 (4.6) |
| real(0,max) | 21428 (1) | 5882 (3.6) | 4285 (5) | 6520 (3.2) | 4688 (4.5) |
| real(min,max) | 18750 (1) | 5084 (3.6) | 3846 (4.8) | 5555 (3.3) | 4225 (4.4) |
native GetRandom_() легче в 3.2 - 6 раз.
Установка
список изменений:
- добавлен LCG, Введение, Описание;
- добавлен LFG, Заключение, тесты на скорость;
- добавлено Дополнительно, изменена работа LFG, подкорректированы тесты на скорость, уменьшен размер файлов.
Скопировать папку LCG/LFG себе в карту.

 WC3
WC3





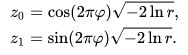
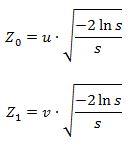

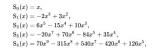



Впрочем, это ничего не решает - всеравно придется жонглировать сидом туда-сюда постоянно, что не очень удобно.