Кривая Безье
Я не буду расписывать какую-либо статью про кривые, какие они бывают, когда кем придуманы и прочую ерунду, ибо в этом нет смысла, всё уже давно разжёвано максимально понятным образом. В самом низу находятся источники, я просто покидаю примеры для понимания. Так же, на хайве есть векторная наработка по кривым с алгоритмом Де Кастельжо:
Зачем?
Это очень простая вещь на самом деле и тем не менее позволяет легко создавать сложные траектории снарядов, которые всем попадались на глаза
Мне необходимо было разобраться как динамически добавлять больше 4 опорных точек для кривой и возникли проблемы, из-за которых пришлось изучать что как где и почему
И да, у меня есть псевдостатья по безье, но мне этого было недостаточно
хотя, скорее всего, и из того, что там есть, можно было сделать безье высшей степени, суммировав значения, но мне не хватило мозгов как всегда
хотя, скорее всего, и из того, что там есть, можно было сделать безье высшей степени, суммировав значения, но мне не хватило мозгов как всегда
Треугольник Паскаля
Для прямого метода нужен треугольник Паскаля:
Делается просто:
private static hashtable PascalTriangle = InitHashtable( )
private static integer PascalTriangleRows = 2
static method RegistPascalTriangle takes integer i returns nothing
local integer n
local integer k
if i > PascalTriangleRows then
set n = PascalTriangleRows
loop
set k = 0
loop
call SaveInteger( PascalTriangle, n, k, LoadInteger( PascalTriangle, n - 1, k - 1 ) + LoadInteger( PascalTriangle, n - 1, k ) )
set k = k + 1
exitwhen k > n
endloop
set n = n + 1
exitwhen n > i
endloop
set PascalTriangleRows = i
endif
endmethod
static method onInit takes nothing returns nothing
call SaveInteger( PascalTriangle, 0, 0, 1 )
call SaveInteger( PascalTriangle, 1, 0, 1 )
call SaveInteger( PascalTriangle, 1, 1, 1 )
endmethodМожно естественно воспользоваться двумерным массивом примерно 7х7, чтобы покрыть практически все нужды и не занимать хэштаблицу, единственная проблема, что массивность двумерных должна быть определена заранее в вджассе, т.е. если есть динамическая фигня и вдруг в игре поднадобилось 8х8+ размерность, то всё сломается
Построение кривой
call RegistPascalTriangle( count )
set i = 0
loop
set r = LoadInteger( PascalTriangle, count - 1, i ) * Pow( 1.00 - time, count - 1 - i ) * Pow( time, i )
set x1 = x1 + r * x[i]
set y1 = y1 + r * y[i]
set z1 = z1 + r * z[i]
set i = i + 1
exitwhen i >= count
endloopcount - количество опорных точек
time - фактор кривой, т.е. нормализированная величина (от 0.00 до 1.00)
x1, y1, z1 - искомая точка
x[ ], y[ ], z[ ] - опорные точки
r - полином, т.е. сама конструкция кривой
time - фактор кривой, т.е. нормализированная величина (от 0.00 до 1.00)
x1, y1, z1 - искомая точка
x[ ], y[ ], z[ ] - опорные точки
r - полином, т.е. сама конструкция кривой
Оптимизация
Чтобы исключить факториалы и треугольники Паскаля, можно воспользоваться алгоритмом Де Кастельжо:
set k = 0
loop
set i = 0
loop
set x[i] = ( 1.00 - time ) * x[i] + time * x[i + 1]
set y[i] = ( 1.00 - time ) * y[i] + time * y[i + 1]
set z[i] = ( 1.00 - time ) * z[i] + time * z[i + 1]
set i = i + 1
exitwhen i > count - k
endloop
set k = k + 1
exitwhen k >= count - 1
endloopВ данном случае опорные точки нужно скопировать, чтобы сохранить основные
В чём преимущества первого метода по сравнению с этим алгоритмом мне не известны
В чём преимущества первого метода по сравнению с этим алгоритмом мне не известны
Прикладываю карту с этими способами

 WC3
WC3





rsfghd:
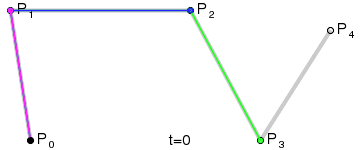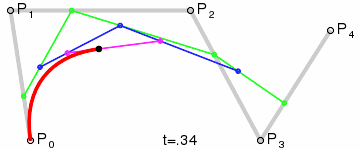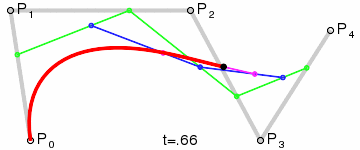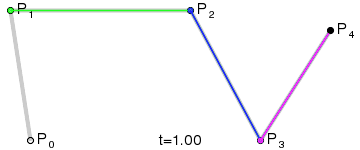
Пример кубической Безье. xgm.guru/files/100/319649/comments/525358/Bezier_example_1.w3m
Тут рабочий просто "бежит" по кривой построенной на основе 4-х точек.
Тут рабочий движется к пехотинцу по воздуху. Из опорных точек можно установить только ту, что в воздухе, указав её высоту и расположение на линии между пехотинцем и рабочим.