Добавлен Castiel
Как реализовать движение по xyz? По xy то понятно, а как быть с вертикальной осью? Не могу сделать движение по прямой из точки x1y1z1 в точку x2y2z2.
Принятый ответ
векторы
library vectors
struct vector
real x
real y
real z
//Статичный метод создающий вектор, принимает координаты возвращает вектор.
//Вектор - отрезок AB, соединяющий из точки A в точку B. Вектор кроме того имеет направление.
//V = (x, y, z) => казалось храним координаты точки, не совсем точно. Храним отрезок с направлением.
//правильнее V = (Bx-Ax, By-Ay, Bz-Az) => из конца вычитаем начало
//эта функция создаем вектор. создается структура, короче выделяется место под массивы. максимум доступно 8190
//прописываем: local vector v = vector.create(0,0,0) <= координаты
static method create takes real x, real y, real z returns vector
local vector v = vector.allocate() // <= что-то вроде перебора индекса массива
set v.x=x
set v.y=y
set v.z=z
return v //<= возвращает на самом деле индекс, номер структуры
endmethod
//Умножает вектор на какое либо число.
//V = V * r
//если раскрыть:
//set v_x[this]=v_x[this] * r
//set v_y[this]=v_y[this] * r
//set v_z[this]=v_z[this] * r
//пишем: local vector v = vector.create(1,1,1)
//пишем: call v.realmul(2) // <= результат вектор с координатами 2 2 2
method realmul takes real r returns nothing
set .x=.x*r
set .y=.y*r
set .z=.z*r
endmethod
//Модуль вектора - метод возвращающий длину вектора (число всегда >0)
//|V| = sqrt(x*x + y*y + z*z)
//пишем: local vector v = vector.create(0,0,1)
//пишем: local real r = v.getlength() <= результат равен 1
method getlength takes nothing returns real
return SquareRoot(.x*.x+.y*.y+.z*.z)
endmethod
//Устанавливет длину вектора равным 1
//Нормализация — приведение к единичному размеру;
//нормализация в трехмерном пространстве - по сути является масштабированием в куб единичного размера
//Для нормализации вектора нужно каждую компоненту поделить на длину вектора, или умножить инверсию длины на данный вектор.
//V/|V| = (x/|V|, y/|V|, z/|V|) <= короче складываем кажду координату, больше вычислении нужно
//set InvLength = 1/legth <=инверсия, здесь меньше вычислении
method normalize takes nothing returns nothing
local real l = .getlength()
if l>0 then
call .realmul(1/l)
endif
endmethod
//Принимает число. Устанавливает длину вектора равной этому числу.
//похожий метод у функции normalize
//пишем: local vector v = vector.create(54,0,0)
//пишем: call v.setlength(30) <= результат: вектор а равен 30 0 0
method setlength takes real r returns nothing
local real l = .getlength()
if l>0 then
call .realmul(r/l)
endif
endmethod
//Принимает вектор. Возвращает число равное скалярному произведению этих векторов.
//Пусть в этом методе A - первый вектор, B - второй вектор (не путайте, выше был предоставлен вектор AB, сейчас поменял обозначения)
// A*B = Ax*Bx + Ay*By + Az*Bz
//используется часто для вычисления углов между векторами
//пишем: local vector v = vector.create(1,2,3)
//пишем: local vector w = vector.create(1,0,3)
//пишем: local real r = v.scalarmul(w)
//результат равен 10
method scalarmul takes vector v returns real
return .x*v.x+.y*v.y+.z*v.z
endmethod
//Принимает вектор. Устанавливает вызывающий вектор равным сумме самого себя и принятого вектора.
//Пусть в этом методе A - первый вектор, B - второй вектор (не путайте, выше был предоставлен вектор AB, сейчас поменял обозначения)
// Bx= Ax+Bx, By= Ay+By, Bz = Az+Bz <= изменяются параметры вектора B
//пишем: local vector v = vector.create(1,2,3)
//пишем: local vector w = vector.create(1,0,3)
//пишем: local real r = v.vectoradd(w)
//результат: вектор v равен 2 2 6, вектор w не изменился
method vectoradd takes vector v returns nothing
set .x=.x+v.x
set .y=.y+v.y
set .z=.z+v.z
endmethod
//аналогично как и метод vectoradd, только вычитывает
method vectorsub takes vector v returns nothing
set .x=.x-v.x
set .y=.y-v.y
set .z=.z-v.z
endmethod
//Принимает вектор. Устанавливает вызывающий вектор равным векторному произведению самого себя и принятого вектора.
//Пусть в этом методе A - первый вектор, B - второй вектор (не путайте, выше был предоставлен вектор AB, сейчас поменял обозначения)
//Bx= (Ay*Bz - By*Az), By= (Az*Bx - Bz*Ax), Bz = (Ax*By - Bx*Ay)
//пишем: local vector v = vector.create(1,0,0)
//пишем: local vector w = vector.create(0,1,0)
//пишем: local real r = v.vectormul(w)
//результат: вектор v равен 0 0 1, вектор w не изменился
method vectormul takes vector v returns nothing
local real x = .y*v.z-v.y*.z
local real y = .z*v.x-v.z*.x
local real z = .x*v.y-v.x*.y
set .x = x
set .y = y
set .z = z
endmethod
//Принимает вектор. Возвращает вектор равный вызывающему.
//Смысл: эта функция создает копию-вектор, который принимает те же значения что у оригинала
//пишем: local vector v = vector.create(1,0,0)
//пишем: local vector w = vector.clone()
//результат: вектор v равен 1 0 0, вектор w равен 1 0 0
method clone takes nothing returns vector
local vector v=vector.allocate()
set v.x=.x
set v.y=.y
set v.z=.z
return v
endmethod
//Принимает вектор. Устанавливает значение вызывающего вектора равным принятому вектору.
//В отличии от метода clone здесь не создается двойник, у нас уже имеется вектор. Не всегда имеет смысл создавать двойников
//пишем: local vector v = vector.create(1,0,0)
//пишем: local vector w = vector.create(0,1,0)
//пишем: call v.copy(w)
//результат: вектор v равен 0 1 0, вектор w равен 0 1 0
method copy takes vector p returns nothing
set .x=p.x
set .y=p.y
set .z=p.z
endmethod
//Принимает координаты x, y и z. Форсированное изменение координат вектора.
//Изменяет текущий вектор.
//пишем: local vector v = vector.create(1,0,0)
//пишем: call v.change(1,1,1)
//результат: вектор v равен 1 1 1
method change takes real x, real y, real z returns nothing
set .x=x
set .y=y
set .z=z
endmethod
//Принимает вектор. Вычисляет угол между двумя векторами.
//Пусть в этом методе A - первый вектор, B - второй вектор (не путайте, выше был предоставлен вектор AB, сейчас поменял обозначения)
//Вытекает из скалярного произведения AB*Cos(A)
//CosA = AB/|A|*|B|, где AB = ax*bx + ay*by + az*bz и |A| = sqrt(ax*ax + ay*ay + az*az), |B| = sqrt(bx*bx + by*by + bz*bz)
method AngleBetweenVectors takes vector b returns real //в радинах
local real ab =.scalarmul(b)/(.getlength()*b.getlength())
return ab
endmethod
method AngleBetweenVectors2 takes vector b returns real //в градусах
local real ab =.scalarmul(b)/(.getlength()*b.getlength())
return Acos(ab)
endmethod
endstruct
endlibrary
пример движения (для новичка), то же самое что и в статье.
хотя я и сам новичок, тк не каждый день приходиться кодить и писать движения. Мне приходится вспоминать свои шпаргалки, или браться за учебники матана.
ниже представлен пример движения снаряда u от u1 (кастера) до u2 (цели)
ниже представлен пример движения снаряда u от u1 (кастера) до u2 (цели)
local unit u1 = GetTriggerUnit()
local unit u2 = GetSpellTargetUnit()
local real x1 = GetUnitX(u1)
local real y1 = GetUnitY(u1)
local real z1 = GetUnitZ(u1)
local real x2 = GetUnitX(u2)
local real y2 = GetUnitY(u2)
local real z2 = GetUnitZ(u2)
local real x
local real y
local real z
local real facing = GetUnitFacing(u1)
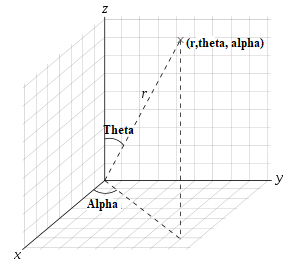
local real apha //угол между точками кастера и цели
local real theta //угол между вектором dz и точкой движения (точнее текущей длиной между точками кастера и цели)
local real dx
local real dy
local real dz
local real dist
local real move_cord = 1000. //move_cord - смещение от начала точки, по-другому можно назвать скоростью speed, если представить окружность то это значение будет радиус-вектором R
if u2 == null then
set x2 = GetSpellTargetX()
set y2 = GetSpellTargetY()
set z2 = GetLocZ(x2,y2)
endif
set dx = (x2-x1)
set dy = (y2-y1)
set dz = (z2-z1)
set dist = SquareRoot( dx*dx + dy*dy )
set alpha = Atan2(dy, dx)
set theta = Atan2(dz, dist)
x = x1 + move_cord * Cos( alpha ) * Sin( theta )
y = y1 + move_cord * Sin( alpha ) * Sin( theta )
z = z1 + move_cord * Cos( theta )
Движение по Z организовывается чуть сложнее, чем в плоскости, из-за особенностей вара:
//инициализация движения
real speed = 1000.0 //скорость движения
//теперь надо преобразовать скорость в вектор движения
real speed_x = speed * Cos(apha) * Sin(theta)
real speed_y = speed * Sin(apha) * Sin(theta)
real speed_z = speed * Cos(theta)
//сохраняем в хеш проекции скорости, и двигаем юнит таймером
//по Z чуть труднее
//не забываем умножать скорость на период таймера
real X = GetUnitX(u) + speed_x * timerPeriod
real Y = GetUnitY(u) + speed_y * timerPeriod
real Z = GetUnitFlyHeight(u) + speed_z * timerPeriod
real land_z = GetLocZ(X,Y) - GetLocZ(GetUnitX(u), GetUnitY(u)) //изменение высот ландшафта между текущей точкой юнита и будущей точкой (X,Y)
SetUnitX(u, X)
SetUnitY(u, Y)
SetUnitFlyHeight(u, Z+land_z, 0)xgm.guru/p/wc3/183641?postid=343279 я собирал кучу наработку движения снарядов. там есть прямые движение по xyz. так вроде недавно видел много наработок и статье по lua
Загруженные файлы
`
ОЖИДАНИЕ РЕКЛАМЫ...
Чтобы оставить комментарий, пожалуйста, войдите на сайт.

 WC3
WC3




Ред. Castiel
Ред. MpW
вот статья из вики
ниже представлен пример движения снаряда u от u1 (кастера) до u2 (цели)