Добавлен WebSter,
опубликован
Анимация от "А" до "Я"
Содержание:
Тип контроллера (Тип Интерполяции)
Контроллер анимации - набор КК, отвечающих за какое-то единственное анимируемое свойство, например, вращение или видимость. Я уже говорил о нём, когда рассказывал про отображение КК определённых объектов.
Тип контроллера (интерполяция) определяет вычисление промежуточных значений между КК. Его можно менять. Для WarCraft III доступны 4 типа контроллеров:
Тип контроллера (интерполяция) определяет вычисление промежуточных значений между КК. Его можно менять. Для WarCraft III доступны 4 типа контроллеров:
- Ступенчатый (None) - вычисление не производится, анимируемый параметр объекта не изменится, пока не встретится новый КК. Когда это произойдёт, он поменяется сразу, рывком - в то значение, которое записано в этом КК;
- Линейный (Linear) - анимируемый параметр между кадрами меняется «линией», т. е. плавно, но без замедления около КК. Этот тип контроллера довольно распространённый, и устанавливается Mdlvis’ом по умолчанию (за исключением контроллера видимости – там Mdlvis устанавливает ступенчатый тип и оперирует только с ним).
- Безье (Bezier) - изменение параметра описывается кривой Безье. Этот тип занимает в 1,5-3 раза больше места, чем линейный и почему-то никак не настраивается в Mdlvis’е. Зато «сглаживает» анимацию вблизи КК, делая движения более естественными и натурально выглядящими. Важно знать, что в игре Безье-вращение не работает (движения не происходят). Используется этот тип контроллера крайне редко – только в некоторых стандартных моделях WarCraft'а, скорее всего потому, что в «полевых условиях» настроить его довольно сложно, но только на первый взгляд.
- Сплайновый (Hermite) - изменение параметра описывается сплайном Эрмита. Это самый сложный и интересный тип интерполяции, позволяющий создавать наиболее естественно выглядящие и качественные анимации, при должном умении, разумеется. Такая интерполяция весит еще больше Безье и используется во многих стандартных моделях WarCraft III. Когда выбран этот тип контроллера, почти во всех КК отображается еще одна панель – «Параметры кривой», в которой можно настраивать свойства сплайна контроллера объекта в каждом КК. Однако, по неизвестным мне причинам, иногда Mdlvis отказывается отображать эту панель в некоторых кадрах. Скорее всего, это связано с недоработанностью сплайновой интерполяции для данной программы, как и писал сам Алексей.
Но тем не менее, работать с ней можно, и далее я расскажу – как.
В некоторых моделях довольно сложно наглядно проследить разницу типов контроллеров, и поэтому, я создал модель простых часов с маятником. Ведь именно на маятнике с минимумом сложностей можно увидеть действие каждой интерполяции.
Заранее замечу, что во вложениях в отдельном архиве (Interpolations.rar) есть 4 модели этих часов с суффиксами, соответствующими интерполяции, которую я использовал для движения маятника, а также модели BezierEllipseOrb.mdx и HermiteEllipseOrb.mdx, в которых показаны примеры Сплайнового и Безье-перемещения, их я буду использовать далее для углублённого изучения данных типов контроллера. Проверять их нужно в редакторе карт или игре! Так как Mdlvis не отображает некоторые баги, w3me может неверно работать со Сплайновой интерполяцией (в контроллере вращения), и только WarCraft покажет истинное положение дел, например то, что тип вращательного контроллера Безье не работает в игре (редакторе). Хотя и в w3me, и в Mdlvis интерполяция Безье отображается совершенно верно (если нет багов в КК, разумеется).
Я думаю, действия ступенчатого и линейного типов не нуждаются в больших подробностях, так как их просто нет, всё описано выше (багов, связанных именно с характерностью интерполяции, в них не наблюдалось), а вот о Безье и сплайновой интерполяциях мы поговорим подробнее.
Безье (Bezier)
Кривая Безье очень часто используется в компьютерной графике, распространяясь от векторных редакторов до создания сплайнов (как статических, так и для анимирования) в приложениях трёхмерного моделирования. И WarCraft III творение Пьера Безье не обошло стороной.
Столкнувшись с ним в Mdlvis'е, не сразу и понимаешь, как оно действует на анимацию – никаких настроек не появляется, а анимация остаётся такой же, как с и линейной интерполяцией. Видимо, Алексей еще не успел внедрить в свою утилиту эти настройки, но я, углубившись в эту тему, нашёл способ настраивать этот тип контроллера вручную и с высокой точностью. Разговор пойдёт о контроллере перемещения, потому что, как я уже говорил, Безье-вращение в игре не работает.
Главная особенность Безье для анимации в WarCraft III - сглаживание углов на линии, по которой мы перемещаем объект, и «выпуклость», т. е. углы сглаживаются не вовнутрь, а наружу, меняя саму линию, а не только её участок рядом с углом
В w3me параметры Безье в каждом КК объекта описываются 3 значениями:
2200: { 0, -1.74099, 60.3338 } | Номер КК и положение объекта в пространстве ({ x, y, z })
InTan: { 0, 29.741, 60.3338 } | Координаты вершины входящей направляющей ({ x, y, z })
OutTan: { 0, -29.741, 60.3338 } | Координаты вершины выходящей направляющей ({ x, y, z })Те, кто работал со сплайнами в 3DS Max, вполне могут провести параллель с кривыми Безье, которые широко используются в нём. Направляющие (2 и 3 на 2.0.1) – это те самые две жёлтые линии с зелёными вершинами на концах. Именно они определяют характер кривой, проводимой между входящей направляющей одной вершины и выходящей направляющей другой.
Рассмотрим их подробнее. Я в 3D Studio Max создал 2 сплайна – ромб, характеризующий движение объекта по своему периметру четырьмя различными КК при линейной интерполяции и тот же ромб, вершинам которого я поставил тип Bezier Corner (входящая и выходящая направляющие независимы друг от друга, как в WarCraft'е), и, настроив их, превратил его в овал. Заметьте, вершин так и осталось 4, т. е. и в игре, движение по периметру такого овала будет тоже характеризоваться четырьмя КК.
Пункт 1 на 2.0.1 – это наша верхняя вершина. При виде спереди справа от неё будет InTan (п. 3 на 2.0.1), т. е. входящая направляющая (не забывайте, что мы рассматриваем её для WarCraft'а, и такое название вовсе не гарантировано в других областях использования кривой Безье), а слева OutTan (п. 2 на 2.0.1) - выходящая направляющая. Двигаясь против часовой стрелки, мы придём во входящую направляющую следующей вершины, т. е. везде "In" стыкуется с "Out" (по часовой стрелке) или "Out" с "In" (против часовой стрелки).
2.0.1
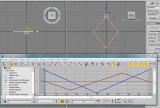
Как же оно действует на анимацию? Очень просто. Представим этот сплайн в виде траектории движения, где вершины – контрольные кадры перемещения (благо в 3DS Max можно без проблем использовать сплайн как траекторию). И перейдём в "Graph Editors/Track view – Curve Editor…", там найдём те параметры, которые мы анимировали, и увидим кривые (у меня это кривые перемещения по оси X и по оси Z (для WarCraft'а роль оси X будет исполнять Y)).
Вот, что мы увидим с обычным ромбом (линейная интерполяция):
2.0.2
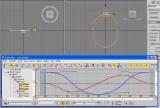
А вот, что с овалом, полученным из ромба благодаря Безье:
2.0.3
Разумеется, углубляться в подробности этих графиков я не буду – всё-таки не о них статья, но я думаю, разница очевидна. Безье позволяет создать из ромба овал, из пары ромбов – восьмёрку и т. д., благодаря такой интерполяции можно делать как жёсткие, так и мягкие движения, сложные траектории, и всё это, обходясь минимумом КК.
Хорошо, с определением типа контроллера мы разобрались, и теперь, думаю, гораздо проще понять его работу и настройки для WarCraft III.
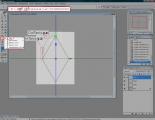
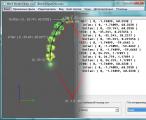
Я не стал придумывать какую-то особую модель и просто взял одну их стандартных игровых сфер с небольшим «хвостом» из частиц, чтобы лучше прослеживать траекторию. Повторив тот самый ромб уже в Mdlvis'е, вот, что мы увидим с линейной интерполяцией (для наглядности я добавил координаты точек и саму траекторию движения на скриншот):
2.0.4
Мы сразу видим углы, причём довольно резко выглядящие при анимации. Увидеть это можно в приложенной модели, установив типом контроллера линейный.
Теперь перейдём в Mdlvis, в Редактор анимаций на вкладку Движение, выберем кость, которую двигали и поставим тип контроллера перемещения – Безье. Пока никаких изменений заметно не будет (потому что направляющие имеют координаты, идентичные вершинам).
И вот сейчас мы подходим к самому важному и интересному.
Для настройки InTan и OutTan нам необходимо узнать координаты направляющих, и здесь, как ни странно, нам придёт на помощь Photoshop (или любой другой редактор, работающий с кривыми Безье, даже MS Word). Установив расположение анимируемой кости во всех КК, я прямо на скриншоте из Mdlvis'а провёл между ними линии, характеризующие траекторию движения (ромб), и, используя инструмент Перо (п. 1 на 2.0.5), провёл линию между двумя точками ромба (верхней и левой), таким образом создав ту самую кривую Безье, которая и должна получиться!
Для настройки InTan и OutTan нам необходимо узнать координаты направляющих, и здесь, как ни странно, нам придёт на помощь Photoshop (или любой другой редактор, работающий с кривыми Безье, даже MS Word). Установив расположение анимируемой кости во всех КК, я прямо на скриншоте из Mdlvis'а провёл между ними линии, характеризующие траекторию движения (ромб), и, используя инструмент Перо (п. 1 на 2.0.5), провёл линию между двумя точками ромба (верхней и левой), таким образом создав ту самую кривую Безье, которая и должна получиться!
Примечание: в настройках инструмента Перо нужно выбирать характер "Пути" (п. 2 на 2.0.5) и тип "Перо" (п. 3 на 2.0.5), а не "Простое перо".
Изменять направляющие можно инструментом Преобразование точки (п. 4 на 2.0.5), как вместе (при нажатии ЛКМ на вершине и движения в разные стороны, не снимая нажатия), так и по отдельности (выделив сами направляющие).
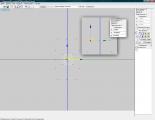
После того, как вы сделали нужную вам кривую, просто на глаз прикиньте координаты направляющих (их точек), у меня это были координаты по осям Y и Z. Если вы затрудняетесь это сделать, можно попробовать создать временные вершины на этих местах прямо в Mdlvis'е и посмотреть их координаты (2.0.6)
2.0.5 | 2.0.6
В принципе, похожие операции можно было произвести в 3DS Max'е, но для этого пришлось бы переносить изображение из окна Mdlvis'а в Макс, потом строить сплайн и пр. На мой взгляд, с Photoshop'ом всё можно сделать быстрее и удобнее.
Я получил координаты { 0, -29, 60 } для OutTan верхней вершины и { 0, -35, 28 } для InTan левой.
Итак, узнав координаты направляющих, нам нужно внести их значения в КК анимируемой кости. Для этого откроем w3me, перейдём в Редактор узлов, затем найдём нашу кость и кликнем ПКМ, выбрав из контекстного меню пункт Редактировать узел. Теперь нажмём кнопку Перенос. Далее ищем требуемые КК (так как кривая строится между двумя точками) и в строках с InTan одного кадра и OutTan другого вводим координаты, которые мы определили ранее. Смело жмём ОК и любуемся (если всё сделано правильно) на получившуюся дугу. Заметьте, именно ту дугу, которую мы строили в 3DS MAx’е и Photoshop’е.
2.0.7
Основываясь на полученных знаниях, я уверен, вы без труда определите координаты оставшихся вершин, а в случае с ромбом их легко просто «угадать».
Важно: значения начального и конечного КК должны точно совпадать! Не являются исключением и значения координат направляющих.
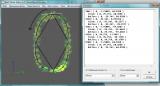
Установив все координаты направляющих для всех КК, можно увидеть окончательный результат – тот самый овал, который мы задумывали изначально.
Установив все координаты направляющих для всех КК, можно увидеть окончательный результат – тот самый овал, который мы задумывали изначально.
2.0.8
По сути, эту интерполяцию можно использовать везде (кроме Вращения), в анимации частиц, текстур, света, цвета и прочего, но принцип остаётся один и тот же, хотя рассчитать значения направляющих иногда бывает очень сложно (бывает, даже представить их не удаётся), тогда часто помогает занимательный "метод тыка".
На этом наше изучение Безье будем считать законченным.
Сплайновая (Hermite)
Такой тип контроллера строится на основе сплайна Эрмита, который я, к сожалению, пока, кроме WarCraft'а, нигде не встречал, и то, как у него рассчитывается кривая, как она зависит от направляющих, мне в большей степени непонятно. И узнать принцип его построения без редактора кривой Mdlvis’а мне выяснить, увы, не удалось, однако, как раз этот редактор кривой и спасает положение. Единственная его проблема – неотображаемость в некоторых кадрах (в 90% случаев в конечном, бывает и/или в начальном).
И еще один главный плюс этой интерполяции для WarCraft’а – это то, что она работает для контроллера вращения. Теперь разберём её основные свойства и пути настройки в Mdlvis’е.
Интерполяция сплайном Эрмита очень похожа на Безье, но отличается менее выраженной выпуклостью, может быть даже сглаживанием углов, настройка в Mdlvis’е проходит в определённых границах, за них вы сможете выйти только вручную, с помощью w3me (1.07 для вращения), ну тут флаг вам в руки…
Интерполяция сплайном Эрмита очень похожа на Безье, но отличается менее выраженной выпуклостью, может быть даже сглаживанием углов, настройка в Mdlvis’е проходит в определённых границах, за них вы сможете выйти только вручную, с помощью w3me (1.07 для вращения), ну тут флаг вам в руки…
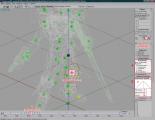
Итак, чтобы настроить кривую в области определённого КК определённой кости и контроллера, вам необходимо: выбрать кость (п. 1 на 2.0.9), выбрать нужный КК (п. 2 на 2.0.9), затем выбрать нужный контроллер (п. 3 на 2.0.9) и определить его тип (п. 4 на 2.0.9), установив выбор на пункте Сплайновый. Теперь у вас должна отобразиться вкладка Параметры кривой.
Если этого не случилось…
…вы сможете «заставить» её отображаться следующим способом:
- Определите КК, в котором не отображаются Параметры кривой.
- Создайте новую локальную анимацию, интервал кадров которой захватывает сбоящий КК (например, если в анимации Stand в кадре 1000 не отображается эта вкладка, создайте анимацию New с интервалом, к примеру, от 700 до 1010). Если после нажатия на кнопку «Создать» вылетела ошибка, просто нажмите ОК, и не обращайте внимания, но можете и перезапустить вис.
- В новой анимации в любом кадре, кроме сбоящего, например 805, произведите движение/вращение/масштабирование для соответствующего контроллера.
- Теперь перейдите на сбоящий кадр, и вуаля – теперь Параметры кривой отображаются!
- Измените их, как вам нужно.
- Затем измените интервал дополнительной анимации так, чтобы сбоящий кадр больше в неё не входил, а дополнительный остался (например, так: от 700 до 999¬).
- Удалите дополнительный кадр.
- Удалите дополнительную анимацию.
Вообще отображение Параметров кривой зависит от наличия соседних КК: если они есть, то Параметры кривой отобразятся, если нет – Mdlvis не высветит их. Так что можете использовать любые альтернативы моему способу.
Интерфейс вкладки Параметры кривой (п. 5 на 2.0.9) состоит из четырёх частей: график кривой (п. 6 на 2.0.9) и три параметра, определяющие её вид - Натяжение (п. 7 на 2.0.9), Целостность (п. 8 на 2.0.9) и Наклон (п. 9 на 2.0.9).
- График кривой представляет собой небольшой прямоугольник, в котором схематично представлен установленный сплайн. Он имеет вид выпуклости и условно разделён на две половины красной линией. Эту линию можно считать своеобразной интерпретацией ключевого кадра, для которого и устанавливается текущий сплайн. Левую часть можно считать в качестве OutTan (как показали тесты на модели с Безье при движении против часовой стрелки), а правую InTan.
- Натяжение - один из параметров кривой, он действует как усилитель или, наоборот, снижает действие Целостности. Если же та равна нулю, то Натяжение определяет замедление вблизи КК, где -100 обозначает его отсутствие, а 100 - максимальный показатель (короткая резкая остановка в КК). Также при значении 100, все остальные параметры автоматически обнуляются. Они полностью зависят от натяжения.
- Целостность - показатель очень похожий на "Bubble" или "Pinch", т. е. он определяет вогнутость или выпуклость обеих ветвей сплайна (на вершину не влияет). Усиливается отрицательными значениями Натяжения.
- Наклон поворачивает ветви сплайна в одну или другую сторону, в зависимости от значения. Он как бы усиливает Целостность на одном участке и ослабляет на другом. Также усиливается отрицательными значениями Натяжения.
2.0.9
Экспериментальным путём я выяснил основные характеристики различных конфигураций Натяжения, Целостности и Наклона кривой. Я использовал только крайние и нулевые значения показателей.
Одиночные сочетания
- Натяжение - острее с предварительным замедлением (+100) или мягче с гладким проходом (-100).
- Целостность +100: небольшая выпуклость перед точкой (провал на точке); -100: аналог Линейной интерполяции.
- Наклон +100: мягкая выпуклость в сторону InTan.
- Наклон -100: мягкая выпуклость в сторону OutTan.
Сочетание Натяжение-Целостность
- Натяжение 100, целостность 100: обнуляется целостность >> п.1.
- Натяжение -100, целостность 100: резкий провал на точке => натяжение усиливает выпуклости по сторонам.
- Натяжение 100, целостность -100: обнуляется целостность >> п.1.
- Натяжение -100, целостность -100: длинные мягкие углубления по сторонам от точки с резким проходом (усиление целостности).
- Натяжение 0, целостность 0: гладкий проход без замедления.
Сочетание Натяжение-Наклон
- Натяжение 100, наклон 100: обнуляется наклон >> п.1.
- Натяжение 100, наклон -100: обнуляется наклон >> п.1.
- Натяжение -100, наклон 100: более крутая мягкая выпуклость в сторону InTan => усиление наклона.
- Натяжение -100, наклон -100: более крутая мягкая выпуклость в сторону OutTan => усиление наклона.
Сочетание Целостность-Наклон
- Целостность 100, наклон 100: выпуклость в сторону InTan с предварительным замедлением.
- Целостность 100, наклон -100: выпуклость в сторону OutTan с предварительным замедлением.
- Целостность -100, наклон 100: небольшое длинное углубление из OutTan, затем стандартный проход в InTan с предварительной резкой остановкой в точке и рывком.
- Целостность -100, наклон -100: небольшое длинное углубление в InTan, затем стандартный проход из OutTan с предварительной резкой остановкой в точке и рывком.
Сочетание Натяжение-Целостность-Наклон
- Натяжение 100, целостность 100 (-100), наклон 100 (-100): обнуляются целостность и наклон >> п.1.
- Натяжение -100, целостность -100, наклон -100: усиление п.17 в сторону InTan - очень резкий рывок после мягкой остановки в точке.
- Натяжение -100, целостность -100, наклон 100: усиление п.16 в сторону OutTan - очень резкий рывок перед мягкой остановкой в точке.
- Натяжение 0, целостность 0, наклон, 0: мягкое длинное замедление в точке.
Следует помнить, что сплайновая интерполяция весьма специфична, и в каждой конкретной ситуации значения кривой могут давать разные результаты.
В приложенной модели HermiteEllipseOrb.mdx вы можете увидеть и даже потренироваться с различными конфигурациями параметров сплайна для контроллера движения с уже знакомым нам овалом и сферой.
Но вернёмся к забытой нами модели маятниковых часов, ведь именно о них я говорил в начале раздела об интерполяции. На их примере мы сможем убедиться в работоспособности и качественности сплайнового типа для контроллера вращения.
Сделав анимацию маятника с помощью линейной интерполяции, я меняю её тип на сплайновый. И тут же встречаюсь с проблемами в начальном и конечном кадре, но в данном случае она исправима довольно простым путём. Так как в анимации происходит 3 движения маятника, одно из них приходится на центр анимации, и, настроив его (Натяжение: -100; Целостность: 0; Наклон: -50) я через w3me 1.07 копирую значения координат вращения, InTan и OutTan начальному и конечному кадру, при этом меняя их значения на противоположные, тем самым получая повторяющуюся кривую, т. е. именно то, что мне и нужно (2.0.10).
Но вполне можно воспользоваться и тем методом, что я приводил выше.
Но вполне можно воспользоваться и тем методом, что я приводил выше.
0: { 0.130526, 0, 0, 0.991445 } | Копируем значения из кадра 500
InTan: { 0.382683, 0, 0, 0.92388 } | и делаем значение X-координат
OutTan: { 0.130526, 0, 0, 0.991445 } | противоположным.
500: { -0.130526, 0, 0, 0.991445 }
InTan: { -0.382683, 0, 0, 0.92388 }
OutTan: { -0.130526, 0, 0, 0.991445 }
1000: { 0.130526, 0, 0, 0.991445 } | Последний кадр должен быть равен начальному,
InTan: { 0.382683, 0, 0, 0.92388 } | поэтому просто копируем его,
OutTan: { 0.130526, 0, 0, 0.991445 } | изменив лишь номер КК (с 0 на 1000).2.0.10
Теперь можно просмотреть анимацию сначала в w3me и Mdlvis’e, а затем в WarCraft 3 World Editor.
Но следует помнить, что со сплайновым типом контроллера тоже сопряжены баги, и часто исправить их бывает очень трудно.
- Довольно распространённая ситуация, когда «на ровном месте», т. е. просто между двумя кадрами появляются странные движения, которых быть не должно. Иногда помогает пересоздание сбоящего кадра путём копирования другого и полностью вручную, иногда спасает ситуацию копирование КК и вставка на один кадр дальше, но бывает так, что и это не помогает.
Частая ошибка в таких ситуациях: человек начинает добавлять один промежуточный кадр, потом еще один, потом еще, и в итоге вместо одного лишнего движения получаются десятки. Этого делать не надо, хотя в крайне редких случаях бывает, что и этот метод помогает.
Одна из вероятных причин такого бага - сочетание сплайновой и линейной интерполяций. Иногда они плохо уживаются вместе, и чтобы избежать подобных вещей необходимо дочерней (иногда и родительской тоже) кости также устанавливать сплайновый тип контроллера. - При копировании КК со сплайновой интерполяцией после вставки значения кривой для вставляемого кадра меняются на "Натяжение: 0; Целостность: -100; Наклон: 0", а у соседних кадров просто сбиваются (кроме значений Натяжение: 0; Целостность: -100; Наклон: 0). Хотя бывает, что сбившиеся настройки дают очень даже неплохие движения. Аналогична ситуация с изменением значения контроллера (т. е. угла поворота, координат перемещения, процентов масштаба и т. д.).
- Вообще, значение кривой "Натяжение: 0; Целостность: -100; Наклон: 0" никогда не даёт никаких багов (по крайней мере, я ни разу не встретил таковых), и его рационально использовать в забагованных местах или для промежуточных стадий в исправлении багов.
- Не стоит доверять w3me при использовании сплайнового контроллера вращения - часто он отображает баги, которых нет, или просто не совсем корректно воспроизводит эти движения.
Использование сплайновой интерполяции, аналогично другим, доступно почти для всех контроллеров, позволяя сделать любую анимацию плавной и живой.
Внимание: в случае использования сплайнового типа контроллера будьте осторожны при оптимизации модели в Mdlvis'е – пункт "Линеаризация анимаций" меняет интерполяцию всех костей на линейную и стирает данные о сплайнах.
Здесь наше изучение интерполяций заканчивается, я надеюсь, что смог грамотно посвятить вас в это непростое дело и что вы будете хотя бы иногда пользоваться чем-то большим, нежели Linear.
Содержание
Чтобы оставить комментарий, пожалуйста, войдите на сайт.

 WC3
WC3





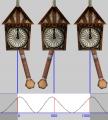
(a) низкое и высокое значения натяжения в центральной точке
(b) низкое и высокое значения непрерывность в центральной точке
(c) низкое и высокое значения наклона в центральной точке
т. е. по идее они весить должны поровну, но так как я не рассматривал безье-вращение ввиду его неработоспособности, то сравнил с безье-перемещением, а оно будет всяко легче, ибо там описываются 3 величины, а во вращении - четыре (x, y, z, w)