MpW
WarCraft 3 Программирование

20. Бинарная арифметика

Добавлен , опубликован

Lua-программирование для чайников

Содержание:
Двоичная арифметика – краткое наименование системы арифметических операций (включающей сложение, вычитание, умножение, деление, иногда некоторые другие операции) над двоичными числами, т.е. целыми числами, представленными в двоичной позиционной системе; собирательное название схемных решений для выполнения арифметических операций над двоичными числами – сумматоров, умножителей, схем вычитания, деления и другие.

Двоичная позиционная система записи целых чисел

Произвольное натуральное число можно единственным способом представить в виде суммы степеней двойки, например 23 = 16+4+2+1.
Обозначая входящие в эту сумму степени двойки единицами, а не входящие в ее степени нулями, можно кратко обозначить эту сумму булевым набором (в другой терминологии - вектором) (10111)2. Индекс 2 напоминает о том, что число записано в двоичной системе. Единица, стоящая в младшем (самом правом) разряде, означает слагаемое 1, единица во втором слева разряде означает слагаемое 2, единица в третьем разряде означает 4, а нуль в четвертом разряде означает отсутствие слагаемого 8, единица в четвертом (старшем) разряде означает присутствие слагаемого 16 (в большинстве случаев разумно рассматривать только такие записи чисел в двоичной системе, в которых в старшем разряде стоит единица).
перевод из десятичной в двоичную:
перевод из двоичной в десятичную:
Главное достоинство двоичной системы (помимо естественности ее применения в электронной цифровой технике ) – исключительная простота алгоритмов арифметических операций в ней.
сложение вычитание умножение деление
0 + 0 = 0 0 - 0 = 0 0 ∙ 0 = 0 0 / 1 = 0
0 + 1= 1 1 - 0 = 1 0 ∙ 1 = 0 1 / 1 =1
1 + 0 = 1 1 - 1 = 0 1 ∙ 0 = 0
1 + 1 = 10 10 - 1 = 1 1 ∙ 1 = 1
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
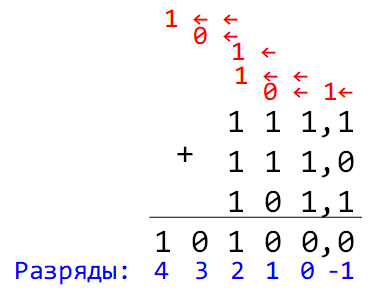
Пример: 1011,1 + 1010,11
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,1 + 111 + 101,1
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают (100)2. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = (101)2. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
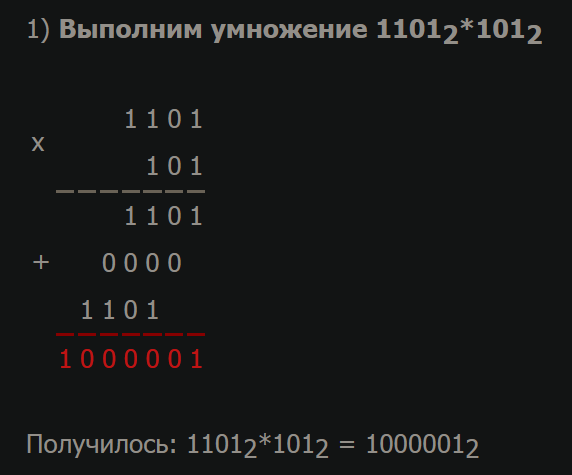
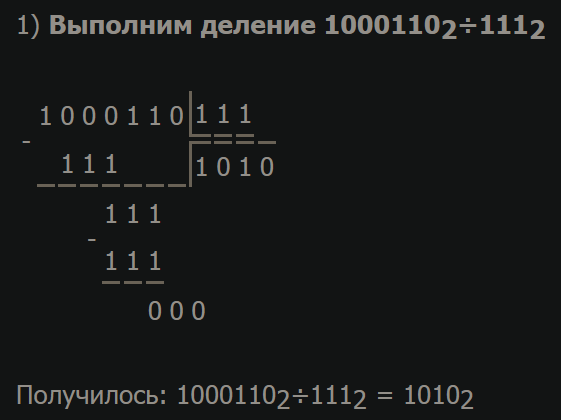
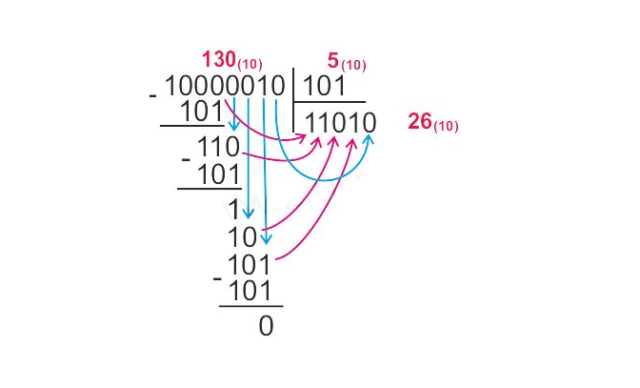
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,01 - 1001,1
Умножение и деление двоичных чисел
калькулятор
Умножение:
Деление:
подробнее, как происходит деление:
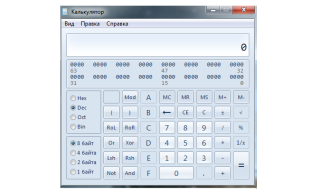
Всегда можно проверить результаты двоичной арифметики с помощью калькулятора. Считать можно и в двоичном формате. Электронный калькулятор в группе стандартных приложений операционной системы MS Windows имеет такой режим работы.

Побитовые операции

источник
Би́товая опера́ция в программировании — операция над цепочками битов, как правило в этот класс включаются логические побитовые операции и битовые сдвиги. Применяются в языках программирования и цифровой технике, изучаются в дискретной математике.
Битовые операции лежат в основе обработки цифровых сигналов: посредством их из одного или нескольких сигналов на входе получается новый сигнал, который в свою очередь может быть подан на вход одной или нескольким таким операциям. Именно битовые операции в сочетании с запоминающими элементами (например триггерами) реализуют всё богатство возможностей современной цифровой техники.
Побитовое отрицание
Побитовое отрицание (или побитовое НЕ, дополнение) — унарная операция, действие которой эквивалентно применению логического отрицания к каждому биту двоичного представления операнда.
Отрицание (инве́рсия)
Отрица́ние (инве́рсия, от лат. inversio — переворот, логи́ческое «НЕ») в логике — унарная операция над суждениями, результатом которой является суждение, «противоположное» исходному. Обозначается знаком ¬ перед или чертой — над суждением.
Как в классической, так и в интуиционистской логике «двойное отрицание» ¬ ¬ A является следствием суждения A, то есть имеет место тавтология: A → ¬ ¬ A .
Обратное утверждение ¬ ¬ A → A верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.

Схема

Мнемоническое правило для отрицания звучит так: на выходе будет
  • «1» тогда и только тогда, когда на входе «0»,
  • «0» тогда и только тогда, когда на входе «1».
A ¬A
0 1
1 0
Другими словами, на той позиции, где в двоичном представлении операнда был 0, в результате будет 1, и, наоборот, где была 1, там будет 0. Например:
НЕ пример 1 пример 2 пример 3
01 11011 10101
итог: 10 00100 01010
Побитовое И
Побитовое «И» — бинарная операция, действие которой эквивалентно применению логического «И» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов.
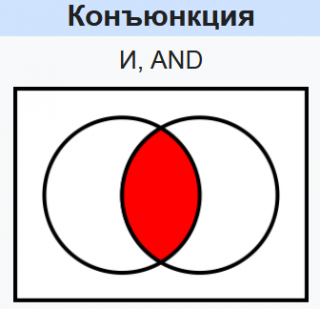
Конъю́нкция (логическое И)
Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Обозначения

Наиболее часто встречаются следующие обозначения для операции конъюнкции:
a ∧ b , a && b , a & b , a ⋅ b , a AND b , min ( a , b )
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab.

Булева алгебра

В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}. Результат также принадлежит множеству {0,1}. Вычисление результата производится по простому правилу, либо по таблице истинности.
Вместо значений 0, может использоваться любая другая пара подходящих символов, например false,true или F,T или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true > false, при цифровом обозначении старшинство естественно 1 > 0.
Правило: результат равен 1, если все операнды равны 1; во всех остальных случаях результат равен 0.

Таблицы истинности

для бинарной конъюнкции
a b a ∧ b
0 0 0
1 0 0
0 1 0
1 1 1
для тернарной конъюнкции
a b с a ∧ b ∧ с
0 0 0 0
1 0 0 0
0 1 0 0
1 1 0 0
0 0 1 0
1 0 1 0
0 1 1 0
1 1 1 1
Другими словами, если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0.
И пример 1 пример 2
первое значение: 0011 1010
второе значение: 0101 1011
итог:: 0001 1010
Побитовое ИЛИ
Побитовое «ИЛИ» — бинарная операция, действие которой эквивалентно применению логического «ИЛИ» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов.
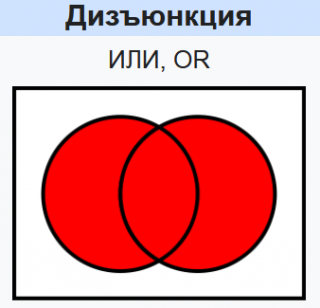
Дизъюнкция
Дизъю́нкция (от лат. disjunctio — «разобщение»), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».
Дизъюнкция может быть операцией как бинарной (имеющей два операнда), так и n-арной (имеющей n операндов) для произвольного n.
Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее.

Обозначения

Наиболее часто встречаются следующие обозначения для операции дизъюнкции:
a ∨ b ,a || b , a | b ,a OR b , max ( a , b ) .

Булева алгебра

Логическая функция MAX в двухзначной (двоичной) логике называется дизъюнкция (логи́ческое «ИЛИ», логи́ческое сложе́ние или просто «ИЛИ»). При этом результат равен наибольшему операнду.
В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Таким образом, результат равен 0, если все операнды равны 0, во всех остальных случаях результат равен 1.

Таблицы истинности

для дизъюнкции
a b a ∨ b
0 0 0
1 0 1
0 1 1
1 1 1
Таблица истинности для тернарной (трёхоперандной) дизъюнкции:
a b с a ∨ b ∨ с
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Другими словами, если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1.
ИЛИ пример 1 пример 2
первое значение: 0011 1010
второе значение: 0101 1011
итог:: 0111 1011
Побитовое исключающее ИЛИ
Побитовое исключающее «ИЛИ» (сложение по модулю 2) — бинарная операция, действие которой эквивалентно применению логического исключающего «ИЛИ» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов.
Другими словами, если оба соответствующих бита операндов равны между собой, двоичный разряд результата равен 0; в противном случае, двоичный разряд результата равен 1.
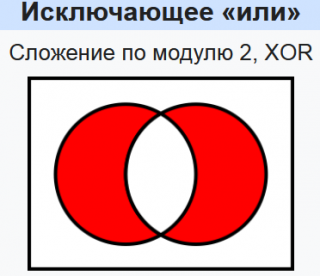
строгая дизъюнкция
Исключа́ющее «или» (сложе́ние по мо́дулю 2, XOR, строгая дизъюнкция, поразрядное дополнение, инвертирование по маске, жегалкинское сложение, логическое вычитание, логи́ческая неравнозна́чность) — булева функция, а также логическая и битовая операция, в случае двух переменных результат выполнения операции истинен тогда и только тогда, когда один из аргументов истинен, а другой — ложен. Для функции трёх (тернарное сложение по модулю 2) и более переменных — результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.

Обозначения

запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:
⊕ 2 ( a , b ) , a ^ b , a ⊕ b , a ⊕ 2 b , a + 2 b , a ≠ b , ( a , b ) ⊕ 2 , a X O R b

Свойства

Булева алгебра

В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}. Результат также принадлежит множеству {0,1}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0 ,1 может использоваться любая другая пара подходящих символов, например false , true или F,T или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true > false.
Таблицы истинности:
для бинарного сложения по модулю 2 (применяется в двоичных полусумматорах)
a b a ⊕ b
0 0 0
1 0 1
0 1 1
1 1 0
Правило: результат равен 0 {\displaystyle 0} {\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1 {\displaystyle 1} 1.
для тернарного сложения по модулю 2 (применяется в двоичных полных сумматорах):
a b с a ⊕ b ⊕ с
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
Правило: результат равен 0, если нет операндов, равных 1, либо их чётное количество (ноль также является чётным числом).
искл. ИЛИ пример 1 пример 2
первое значение: 0011 1010
второе значение: 0101 1011
итог:: 0110 1001
битовый сдвиг
К битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов.
Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).
источник
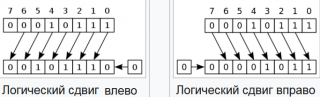
Логический сдвиг
Сдвиг, при котором уходящий бит исчезает, не влияя на оставшиеся биты, а на месте появившегося бита записывается бит 0.
Пример работы операции сдвига:
  • Пусть у нас есть число 10101010b (в двоичной системе).
  • Если сделать сдвиг влево на 1 бит, то получим число 01010100b.
  • Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 01010101b.
В большинстве процессоров уходящий бит сохраняется во флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.
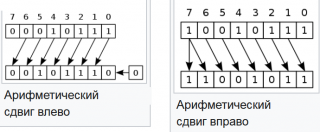
Арифметический сдвиг
При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо уходящий бит исчезает, не влияя на оставшиеся биты, а на месте появившегося бита устанавливается бит, соответствующий знаку.

Пример № 1

Пример работы операции сдвига 8 битного числа в прямом коде:
  • Пусть у нас есть 8 битное число: 00000010b = 2. (записанное в двоичной системе, в прямом коде).
  • Cдвиг влево на 1 бит, даёт число: 00000100b = 4.
  • Сдвиг вправо на 1 бит, даёт число: 00000001b = 1.

Пример № 2

Пример работы операции сдвига 8 битного числа записанного в дополнительном до 2х коде:
  • Пусть у нас есть число 11111010b = −6 (в двоичной системе, в дополнительном коде).
  • Если сделать сдвиг влево на 1 бит, то получим число 11110100b = −12.
  • Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 11111101b = −3.

Вывод

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо — делению на 2 (в общем случае — на основание системы счисления) с округлением к −∞. Например:
1011 = −5 1111 = −1
>>a 1 >>a 1
---- ----
1101 = −3 1111 = −1
Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа, равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.) — если, конечно, такое округление отрицательных чисел не мешает.
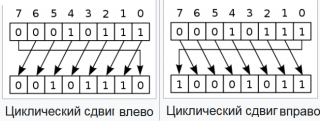
Циклический сдвиг
При этом сдвиге уходящий бит появляется на месте появившегося свободного на другом конце числа.
== Пример ==
  • Пусть у нас есть число 11111010b (в двоичной системе).
  • Если сделать сдвиг влево на 1 бит, то получим число 11110101b.
  • Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 01111101b.
Циклический сдвиг через бит переноса
В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на x86). Данная операция выполняет циклический сдвиг над (n+1)-битным числом, состоящим из регистра и флага переноса.
Например, если у нас в регистре число 11111010b, флаг переноса циклического сдвига вправо равен 0.
После сдвига влево на 1 бит в регистре 11110101b, флаг переноса равен 1.
Далее, после сдвига вправо на 1 бит в регистре 01111101b, флаг переноса равен 1.
Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1] cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Было: HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI: HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED: HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO: HI=0011, MED=0001, LO=1110, cf=0
Сдвиги через регистр флагов более чем на 1 бит практически не используются.
В lua программирования
print(3 & 5)  -- bitwise and
print(3 | 5)  -- bitwise or
print(3 ~ 5)  -- bitwise xor
print(7 >> 1) -- bitwise right shift
print(7 << 1) -- bitwise left shift
print(~7)     -- bitwise not
выдаст результат
1
7
6
3
14
-8
В рефордже есть нативки:
--  Bit Operations

---@param x integer
---@param y integer
---@return integer
function BlzBitOr(x, y) end	-- (native)

---@param x integer
---@param y integer
---@return integer
function BlzBitAnd(x, y) end	-- (native)

---@param x integer
---@param y integer
---@return integer
function BlzBitXor(x, y) end	-- (native)
Пример Unryze на мемхаке (Скинул сюда чтобв не уплыла в переписке):
BitwiseOR для записи в integer, BitwiseAND для чтения. Таким образом можно записывать флаги в целое число, и наоборот доставать.
int a = BitwiseOr( 1, 2 ) получаем 3.
bool check = BitwiseAND( 3, 2 ) проверяет содержит ли наш флаг, флаг 2.
В луа можно проверять флаги. Вернет 1, если галочка отмечена, или 0, если не стоит. Код Прометея:
	function IsFlagSet(flags, pos)
		if pos == nil then
			return false
		else
			return flags >> pos & 1 == 1
		end
	end
или
пример чтение флага из целого числа
Допустим:
flag = 7 - это целое число
есть типы проходимости в варкрафте. ну допустим:
Цель земля = 1 (2^0=1)
Цель воздух = 2 (2^1=2)
Цель вода = 4 (2^2=4)
данные раскладываем на степени 2.
local flag = 7
if (flag & 1 == 1 ) and (flag & 2 == 2 ) and (flag & 4 == 4 ) then
   print('true')
end

print(flag & 3 == 3 ) --вернет истину, так как из 1+2+4 возможно получить 3. это 1+2
print(flag & 5 == 5 ) --вернет истину, так как из 1+2+4 возможно получить 5. это 1+4
можно это условие обернуть в обертку для удобства:
--где bits и flag - это integer
function IsFlagBitSet(bits, flag)
	return ( bits & flag ) == flag
end
пример флаги
удобно хранить все флаги в одной глобалке. пример, есть требования в варкрафте по строительству здании в определенных типах паффинга:
	--двоичный код
    ground = 1     --ground-pathable PATHING_TYPE_WALKABILITY   
    air = 2        --air-pathable PATHING_TYPE_FLYABILITY          
    buildable = 4  --buildable PATHING_TYPE_BUILDABILITY
    unblighted = 8 --unblighted PATHING_TYPE_BLIGHTPATHING 
    sea = 16        --sea-pathable PATHING_TYPE_FLOATABILITY
    amphibious = 32 --amphibious-pathable PATHING_TYPE_AMPHIBIOUSPATHING

	--инициирую таблицу, где будет забита база данных
	build_pathing_placement_resqures = {}
    --peasant (human)
    build_pathing_placement_resqures[FourCC('htow')]=buildable
    build_pathing_placement_resqures[FourCC('hhou')]=buildable
    build_pathing_placement_resqures[FourCC('hbar')]=buildable
    build_pathing_placement_resqures[FourCC('hbla')]=buildable
    build_pathing_placement_resqures[FourCC('hwtw')]=buildable
    build_pathing_placement_resqures[FourCC('halt')]=buildable
    build_pathing_placement_resqures[FourCC('harm')]=buildable
    build_pathing_placement_resqures[FourCC('hars')]=buildable
    build_pathing_placement_resqures[FourCC('hlum')]=buildable
    build_pathing_placement_resqures[FourCC('hgra')]=buildable
    build_pathing_placement_resqures[FourCC('hvlt')]=buildable
    --peon (orc)
    build_pathing_placement_resqures[FourCC('ogre')]=buildable
    build_pathing_placement_resqures[FourCC('otrb')]=buildable
    build_pathing_placement_resqures[FourCC('obar')]=buildable
    build_pathing_placement_resqures[FourCC('ofor')]=buildable
    build_pathing_placement_resqures[FourCC('oalt')]=buildable
    build_pathing_placement_resqures[FourCC('obea')]=buildable
    build_pathing_placement_resqures[FourCC('osld')]=buildable
    build_pathing_placement_resqures[FourCC('otto')]=buildable
    build_pathing_placement_resqures[FourCC('owtw')]=buildable
    build_pathing_placement_resqures[FourCC('ovln')]=buildable
если нужно указать несколько флагов, то складываем:
	--пример air+buildable=2+4=6
	build_pathing_placement_resqures[FourCC('htow')]=air+buildable
	
	--или пример ground+air+buildable=1+2+4=7
	build_pathing_placement_resqures[FourCC('hhou')]=ground+air+buildable
если нужно проверить флаги, можно использовать спец функцию:
function check_pathing_placement_resqures(x,y,flag) 

	if flag & 1 == 1 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_WALKABILITY)) then
		   return false
	   end
	end
	if flag & 2 == 2 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_FLYABILITY)) then
		   return false
	   end
	end
	if flag & 4 == 4 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_BUILDABILITY)) then
		   return false
	   end
	end
	if flag & 8 == 8 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_BLIGHTPATHING)) then
		   return false
	   end
	end
	if flag & 16 == 16 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_FLOATABILITY)) then
		   return false
	   end
	end
	if flag & 32 == 32 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_AMPHIBIOUSPATHING)) then
		   return false
	   end
	end
	
	return true
end
запрет строить в опред типе паффинге
аналогично и с запретом строить в определенном месте, как пример у нежити запрещено строить не на порче.
	build_pathing_placement_prevented_by = {}
    --acolyte (undead)
    build_pathing_placement_prevented_by[FourCC('uzig')]=unblighted
    build_pathing_placement_prevented_by[FourCC('usep')]=unblighted
    build_pathing_placement_prevented_by[FourCC('ugrv')]=unblighted
    build_pathing_placement_prevented_by[FourCC('uaod')]=unblighted
    build_pathing_placement_prevented_by[FourCC('utod')]=unblighted
    build_pathing_placement_prevented_by[FourCC('uslh')]=unblighted
    build_pathing_placement_prevented_by[FourCC('ubon')]=unblighted
    build_pathing_placement_prevented_by[FourCC('usap')]=unblighted
    build_pathing_placement_prevented_by[FourCC('utom')]=unblighted
если нужно проверить флаги, можно использовать спец функцию:
function check_pathing_placement_prevented_by(x,y,flag) 

	if flag & 1 == 1 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_WALKABILITY)) then
		   return false
	   end
	end
	if flag & 2 == 2 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_FLYABILITY)) then
		   return false
	   end
	end
	if flag & 4 == 4 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_BUILDABILITY)) then
		   return false
	   end
	end
	if flag & 8 == 8 then
	   if (IsTerrainPathable(x, y, PATHING_TYPE_BLIGHTPATHING)) then
		   return false
	   end
	end
	if flag & 16 == 16 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_FLOATABILITY)) then
		   return false
	   end
	end
	if flag & 32 == 32 then
	   if not(IsTerrainPathable(x, y, PATHING_TYPE_AMPHIBIOUSPATHING)) then
		   return false
	   end
	end
	
	return true
end
Применении двоичной алгебры я мало знаю.
пример в атаке
Аналогично, можно использовать, склеивая условия. Пример:
	function GetBooleanAnd(valueA, valueB)
	    return valueA and valueB
	end
	function GetBooleanOr(valueA, valueB)
	    return valueA or valueB
	end

Содержание
8 июл 2022
26 076
`
ОЖИДАНИЕ РЕКЛАМЫ...
Чтобы оставить комментарий, пожалуйста, войдите на сайт.