Добавлен nvc123,
опубликован
Раздел:
Триггеры и объекты
Примечание
В Warcraft III функции Sin и Cos принимают углы в радианах, поэтому, чтобы правильно оперировать с углами в градусах (например, взятый угол поворота юнита), нужно умножать их на bj_DEGTORAD.
Пример:
Пример:
local real a = GetUnitFacing(u)
local real distance = 1000.0
local real vec_x = distance * Cos(a * bj_DEGTORAD)
local real vec_y = distance * Sin(a * bj_DEGTORAD)— прим. ScorpioT1000
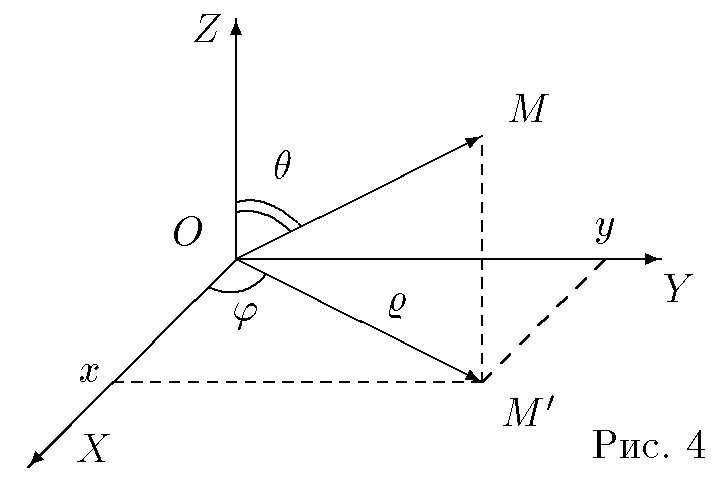
Что такое сферические координаты
Итак, частным случаем сферических координат являются полярные координаты (угол плюс расстояние) данные координаты позволяют очень удобно и гибко работать с перемещениями в 2d (да и не только с ними), в сферических же координатах добавляться еще один угол, в результате мы получаем 3d аппарат.
Как это выглядит?
Итак, там есть два угла, нижний (который фи) это известный нам угол полярных координат, а вот верхний (тета) тот самый введенный, в классике, как на картинке, это угол между направлением "вверх" и направлением к точке (чьи координаты мы хотим представить), так же существует и система координат, где угол берётся между направлением и проекцией на плоскость.
Формулы перехода
Для полярных координат это:
set x = p * Cos( a )
set y = p * Sin( a )Для сферических все не намного сложнее:
set x = p * Cos( a ) * Sin( t )
set y = p * Sin( a ) * Sin( t )
set z = p * Cos( t )t - новый угол, эти формулы для классики, для второй системы координат достаточно поменять синус и косинус введенного угла местами.
Для чего это нужно
Ну спектр применения довольно широк, например когда нужно, чтоб огненный шарик летел не просто в точку с координатами X и Y, но и учитывалась высоты этой точки. В общем там где высота имеет значение.
Еще одна формула
Просто для общего развития (тех кто не знает само собой :):).
Формула расстояния d 3d
Формула расстояния d 3d
set p = SquareRoot( dx * dx + dy * dy + dz * dz) Где dx, dy, dz - соответствующая разница координат.
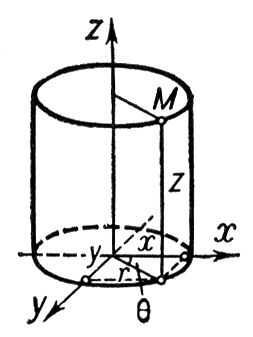
Цилиндрические координаты
Но не всегда 3d удобно представлять в виде сферы. Пример такого неудобства всевозможные спирали вокруг юнита и так далее. Интуитивно многие приходили к этой системе. И она несколько проще для понимания.
Как это выглядит?
разберемся чем это отличается от сферических координат? В основе все та же полярка, а вот 3я координата вводиться просто и без заумностей, как высота.
Формулы перехода
Формулы тут тоже гораздо проще:
set x = p * Cos( a )
set y = p * Sin( a )
set z = hТут угол а - угол полярных координат, h - высота точки, p - длинна проэкции на плоскость.
Для чего это нужно
С помощью цилиндрических координат решаются те же задачи что и с помощью сферических, тут стоит вопрос удобства. Например реализация движения по поверхности сферы это удобнее в сферических, а по поверхности цилиндра это в цилиндрических.
Что такое повороты и с чем их едят
Иногда не очень удобно использовать ту или иную систему координат "как есть".
Например задача: построить окружность в плоскости отличной от горизонтальной.
На первый взгляд решение стоит копать в сторону сферических координат... Но нахождение параметрического уравнения такой окружности в сферических координатах не такая уж простая задача, гораздо удобнее и быстрее (как в человеческом понимании, так и в машинном) работать с поворотами.
Например задача: построить окружность в плоскости отличной от горизонтальной.
На первый взгляд решение стоит копать в сторону сферических координат... Но нахождение параметрического уравнения такой окружности в сферических координатах не такая уж простая задача, гораздо удобнее и быстрее (как в человеческом понимании, так и в машинном) работать с поворотами.
Что нам нужно?
Для начала разберемся, что же задает плоскость в пространстве? Для наших целей подойдет 2 угла (a и b) и точка t.
t - точка через которую проходит горизонтальная плоскость (которую и будем поворачивать)
a - угол поворота вокруг оси, параллельной X, проходящей через t
b - угол поворота вокруг оси, параллельной Z, проходящей через t
(на самом деле можно брать любые 2 оси)
Таким образом можно задать любую плоскость в пространстве.
t - точка через которую проходит горизонтальная плоскость (которую и будем поворачивать)
a - угол поворота вокруг оси, параллельной X, проходящей через t
b - угол поворота вокруг оси, параллельной Z, проходящей через t
(на самом деле можно брать любые 2 оси)
Таким образом можно задать любую плоскость в пространстве.
Формулы перехода
Перейдем к формулам.
Пусть есть две точки t1 и t2, и угол на который надо повернуть t2 относительно t1 (пусть это будет угол a) вокруг какой-то оси. Тогда формулы поворота будут иметь вид:
Пусть есть две точки t1 и t2, и угол на который надо повернуть t2 относительно t1 (пусть это будет угол a) вокруг какой-то оси. Тогда формулы поворота будут иметь вид:
//вокруг оси X:
set x' = x2
set y' = y1 + (y2 - y1) * Cos( a ) + (z1 - z2) * Sin( a )
set z' = z1 + (y2 - y1) * Sin(a ) + (z2 - z1) * Cos( a )
//вокург оси Y:
set x' = x1 + (x2 - x1) * Cos( a ) + (z1 - z2) * Sin( a )
set y' = y2
set z' = z1 + (x2 - x1) * Sin( a ) + (z2 - z1) * Cos( a )
//вокруг оси X:
set x' = x1 + (x2 - x1) * Cos( a ) + (y2 - y1) * Sin( a )
set y' = y1 + (x2 - x1) * Sin( a ) + (y1 - y2) * Cos( a )
set z' = z2
Здесь x', y' и z' - новые координаты точки t2.
Опять к окружностям
Вернемся к нашей задаче. С помощью поворотов и можно построить окружность с центром в какой либо точке и произвольным наклоном. Что для этого нужно? Не так много. Построить окружность с помощью 2d координат, и подействовать на них последовательно двумя поворотами относительно двух любых осей на требуемые углы.
На самом деле мы опять придем к сферической системе координат, но как бы с задней двери.
На самом деле мы опять придем к сферической системе координат, но как бы с задней двери.
В примере показаны юниты летающие по поверхности цилиндра и сферы (в 2х вариациях: через сферические координаты и повороты полярной системы координат).
Каждые 5 секунд будут создаться по одному юниту для каждой системы координат.
Каждые 5 секунд будут создаться по одному юниту для каждой системы координат.
Выкладываю пример движения по параболе. Основано на векторах, пока без комментариев и дополнений к статье.
Чтобы оставить комментарий, пожалуйста, войдите на сайт.

 WC3
WC3



в сферических координатах не такая уж простая задача...
НИЧЕГО ПОДОБНОГО! Сделал !
Отредактирован Rewenger